Esempio di deviazione standard. Cos'è la deviazione standard: utilizzo della funzione deviazione standard per calcolare la deviazione standard in Excel

Un metodo approssimativo per valutare la variabilità di una serie di variazioni consiste nel determinare il limite e l'ampiezza, ma i valori della variante all'interno della serie non vengono presi in considerazione. La principale misura generalmente accettata della variabilità di una caratteristica quantitativa all'interno di una serie di variazioni è deviazione standard (σ - sigma). Maggiore è la deviazione standard, maggiore è il grado di fluttuazione di questa serie.

Il metodo per il calcolo della deviazione standard prevede i seguenti passaggi:

1. Trova la media aritmetica (M).

2. Determinare le deviazioni delle singole opzioni dalla media aritmetica (d=V-M). Nelle statistiche mediche, le deviazioni dalla media sono designate come d (deviare). La somma di tutte le deviazioni è zero.

3. Eleva al quadrato ogni deviazione d 2.

4. Moltiplicare i quadrati delle deviazioni per le frequenze corrispondenti d 2 *p.

5. Trova la somma dei prodotti å(d 2 *p)

6. Calcola la deviazione standard utilizzando la formula:

Quando n è maggiore di 30 o quando n è minore o uguale a 30, dove n è il numero di tutte le opzioni.

Valore della deviazione standard:

1. La deviazione standard caratterizza la diffusione della variante rispetto al valore medio (cioè la variabilità della serie di variazioni). Più grande è il sigma, maggiore è il grado di diversità di questa serie.

2. La deviazione standard viene utilizzata per una valutazione comparativa del grado di corrispondenza della media aritmetica con la serie di variazioni per la quale è stata calcolata.

Le variazioni dei fenomeni di massa obbediscono alla legge della distribuzione normale. La curva che rappresenta questa distribuzione sembra una curva simmetrica liscia a forma di campana (curva gaussiana). Secondo la teoria della probabilità, nei fenomeni che obbediscono alla legge della distribuzione normale, esiste una stretta relazione matematica tra i valori della media aritmetica e della deviazione standard. La distribuzione teorica di una variante in una serie di variazioni omogenee obbedisce alla regola dei tre sigma.

Se in un sistema di coordinate rettangolari i valori di una caratteristica quantitativa (varianti) sono tracciati sull'asse delle ascisse e la frequenza con cui si verifica una variante in una serie di variazioni è tracciata sull'asse delle ordinate, allora le varianti con maggiore e minore i valori si trovano uniformemente ai lati della media aritmetica.

È stato stabilito che con una distribuzione normale del tratto:

Il 68,3% dei valori delle varianti rientra in M±1s

Il 95,5% dei valori delle varianti rientra in M±2s

Il 99,7% dei valori delle varianti sono compresi tra M±3s

3. La deviazione standard consente di stabilire valori normali per i parametri clinici e biologici. In medicina, l'intervallo M±1s viene solitamente considerato l'intervallo normale per il fenomeno studiato. La deviazione del valore stimato dalla media aritmetica di più di 1 s indica una deviazione del parametro studiato dalla norma.

4. In medicina, la regola dei tre sigma viene utilizzata in pediatria per la valutazione individuale del livello di sviluppo fisico dei bambini (metodo della deviazione sigma), per lo sviluppo di standard per l'abbigliamento per bambini

5. La deviazione standard è necessaria per caratterizzare il grado di diversità della caratteristica studiata e per calcolare l'errore della media aritmetica.

Il valore della deviazione standard viene solitamente utilizzato per confrontare la variabilità di serie dello stesso tipo. Se si confrontano due serie con caratteristiche diverse (altezza e peso, durata media del trattamento ospedaliero e mortalità ospedaliera, ecc.), allora un confronto diretto delle dimensioni sigma è impossibile , Perché la deviazione standard è un valore denominato espresso in numeri assoluti. In questi casi, utilizzare coefficiente di variazione (Cv), che è un valore relativo: il rapporto percentuale tra la deviazione standard e la media aritmetica.

Il coefficiente di variazione si calcola utilizzando la formula:

Maggiore è il coefficiente di variazione , maggiore è la variabilità di questa serie. Si ritiene che un coefficiente di variazione superiore al 30% indichi l'eterogeneità qualitativa della popolazione.

$X$. Per cominciare, ricordiamo la seguente definizione:

Definizione 1

Popolazione- un insieme di oggetti selezionati casualmente di un dato tipo, sui quali vengono effettuate osservazioni per ottenere valori specifici di una variabile casuale, effettuate in condizioni costanti durante lo studio di una variabile casuale di un dato tipo.

Definizione 2

Varianza generale-- la media aritmetica delle deviazioni al quadrato dei valori della variante della popolazione dal loro valore medio.

Supponiamo che i valori dell'opzione $x_1,\ x_2,\dots ,x_k$ abbiano rispettivamente frequenze $n_1,\ n_2,\dots ,n_k$. Quindi la varianza generale viene calcolata utilizzando la formula:

Consideriamo un caso speciale. Lascia che tutte le opzioni $x_1,\ x_2,\dots,x_k$ siano diverse. In questo caso $n_1,\ n_2,\dots ,n_k=1$. Troviamo che in questo caso la varianza generale è calcolata con la formula:

Questo concetto è anche associato al concetto di deviazione standard generale.

Definizione 3

Deviazione standard generale

\[(\sigma )_g=\sqrt(D_g)\]

Varianza di campionamento

Sia data una popolazione campione rispetto ad una variabile casuale $X$. Per cominciare, ricordiamo la seguente definizione:

Definizione 4

Popolazione campione- parte di oggetti selezionati dalla popolazione generale.

Definizione 5

Varianza di campionamento-- media aritmetica dei valori della popolazione campione.

Supponiamo che i valori dell'opzione $x_1,\ x_2,\dots ,x_k$ abbiano rispettivamente frequenze $n_1,\ n_2,\dots ,n_k$. Quindi la varianza campionaria viene calcolata utilizzando la formula:

Legato a questo concetto è anche il concetto di deviazione standard campionaria.

Definizione 6

Deviazione standard del campione-- radice quadrata della varianza generale:

\[(\sigma )_â=\sqrt(D_â)\]

Varianza corretta

Per trovare la varianza corretta $S^2$ è necessario moltiplicare la varianza campionaria per la frazione $\frac(n)(n-1)$, ovvero

A questo concetto è associato anche il concetto di deviazione standard corretta, che si trova nella formula:

Nel caso in cui i valori delle varianti non siano discreti, ma rappresentino intervalli, nelle formule per il calcolo delle varianze generali o campionarie, il valore di $x_i$ viene considerato il valore del centro dell'intervallo a a cui appartiene $x_i.$.

Un esempio di problema per trovare la varianza e la deviazione standard

Esempio 1

La popolazione campione è definita dalla seguente tabella di distribuzione:

Immagine 1.

Troviamo la varianza campionaria, la deviazione standard campionaria, la varianza corretta e la deviazione standard corretta.

Per risolvere questo problema, creiamo innanzitutto una tabella di calcolo:

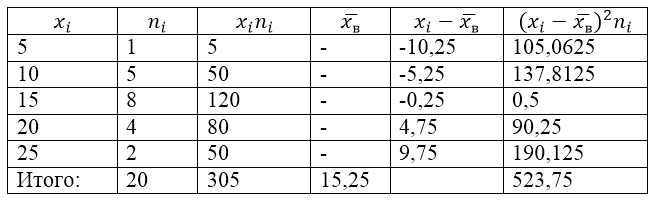
Figura 2.

Il valore $\overline(x_â)$ (media campionaria) nella tabella si trova con la formula:

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]

Troviamo la varianza campionaria utilizzando la formula:

Deviazione standard del campione:

\[(\sigma )_â=\sqrt(D_â)\circa 5,12\]

Varianza corretta:

\[(S^2=\frac(n)(n-1)D)_â=\frac(20)(19)\cdot 26.1875\circa 27.57\]

Deviazione standard corretta.

Lezione n.4

Argomento: “Statistica descrittiva. Indicatori di diversità dei tratti nel complesso"

I criteri principali per la diversità di una caratteristica in una popolazione statistica sono: limite, ampiezza, deviazione standard, coefficiente di oscillazione e coefficiente di variazione. Nella lezione precedente, è stato discusso che i valori medi forniscono solo una caratteristica generalizzata della caratteristica studiata nel complesso e non tengono conto dei valori delle sue varianti individuali: valori minimo e massimo, sopra la media, sotto media, ecc.

Esempio. Valori medi di due diverse sequenze numeriche: -100; -20; 100; 20 e 0,1; -0,2; 0.1 sono assolutamente identici e ugualiDI.Tuttavia, gli intervalli di dispersione di questi dati di sequenza media relativa sono molto diversi.

La determinazione dei criteri elencati per la diversità di una caratteristica viene effettuata principalmente tenendo conto del suo valore nei singoli elementi della popolazione statistica.

Gli indicatori per misurare la variazione di un tratto sono assoluto E parente. Gli indicatori assoluti di variazione includono: intervallo di variazione, limite, deviazione standard, dispersione. Il coefficiente di variazione e il coefficiente di oscillazione si riferiscono a misure relative di variazione.

Limite (lim)– Questo è un criterio determinato dai valori estremi di una variante in una serie di varianti. In altre parole, questo criterio è limitato ai valori minimo e massimo dell'attributo:

Ampiezza (Am) O gamma di variazione – Questa è la differenza tra le opzioni estreme. Il calcolo di questo criterio viene effettuato sottraendo il suo valore minimo dal valore massimo dell'attributo, che consente di stimare il grado di dispersione dell'opzione:

Lo svantaggio del limite e dell'ampiezza come criteri di variabilità è che dipendono completamente dai valori estremi della caratteristica nella serie di variazioni. In questo caso non vengono prese in considerazione le fluttuazioni dei valori degli attributi all'interno di una serie.

La descrizione più completa della diversità di un tratto in una popolazione statistica è fornita da deviazione standard(sigma), che è una misura generale della deviazione di un'opzione dal suo valore medio. Viene spesso chiamata deviazione standard deviazione standard.

La deviazione standard si basa sul confronto di ciascuna opzione con la media aritmetica di una data popolazione. Poiché nell'insieme ci saranno sempre opzioni sia inferiori che superiori, la somma delle deviazioni con il segno "" verrà cancellata dalla somma delle deviazioni con il segno "", ad es. la somma di tutte le deviazioni è zero. Per evitare l'influenza dei segni delle differenze, vengono prese le deviazioni dalla media aritmetica al quadrato, ad es. . La somma delle deviazioni quadrate non è uguale a zero. Per ottenere un coefficiente in grado di misurare la variabilità, prendi la media della somma dei quadrati: questo valore viene chiamato varianze:

In sostanza la dispersione è il quadrato medio degli scostamenti dei singoli valori di una caratteristica dal suo valore medio. Dispersione – quadrato della deviazione standard.

La varianza è una quantità dimensionale (denominata). Quindi, se le varianti di una serie numerica sono espresse in metri, allora la varianza dà i metri quadrati; se le opzioni sono espresse in chilogrammi, la varianza dà il quadrato di questa misura (kg 2), ecc.

Deviazione standard– radice quadrata della varianza:

, quindi quando si calcola la dispersione e la deviazione standard nel denominatore della frazione, invece dideve essere posizionato.

Il calcolo della deviazione standard può essere suddiviso in sei fasi, che devono essere eseguite in una determinata sequenza:

Applicazione della deviazione standard:

a) per giudicare la variabilità delle serie di variazioni e valutare comparativamente la tipicità (rappresentatività) delle medie aritmetiche. Ciò è necessario nella diagnosi differenziale quando si determina la stabilità dei sintomi.

b) ricostruire la serie di variazioni, ovvero ripristino della sua risposta in frequenza basata su tre regole sigma. Nell'intervallo (М±3σ) Il 99,7% di tutte le varianti della serie si trovano nell'intervallo (М±2σ) - 95,5% e nell'intervallo (М±1σ) - Variante di riga 68,3%.(Fig. 1).

c) identificare le opzioni “pop-up”.

d) determinare i parametri di norma e patologia utilizzando stime sigma

e) calcolare il coefficiente di variazione

f) calcolare l'errore medio della media aritmetica.

Per caratterizzare qualsiasi popolazione che abbiatipo di distribuzione normale , è sufficiente conoscere due parametri: la media aritmetica e la deviazione standard.

Figura 1. Regola dei tre Sigma

Esempio.

In pediatria, la deviazione standard viene utilizzata per valutare lo sviluppo fisico dei bambini confrontando i dati di un particolare bambino con i corrispondenti indicatori standard. Come standard viene presa la media aritmetica dello sviluppo fisico dei bambini sani. Il confronto degli indicatori con gli standard viene effettuato utilizzando tabelle speciali in cui gli standard sono forniti insieme alle corrispondenti scale sigma. Si ritiene che se l'indicatore dello sviluppo fisico del bambino rientra nello standard (media aritmetica) ±σ, allora lo sviluppo fisico del bambino (secondo questo indicatore) corrisponde alla norma. Se l'indicatore rientra nello standard ±2σ, si verifica una leggera deviazione dalla norma. Se l'indicatore supera questi limiti, lo sviluppo fisico del bambino differisce nettamente dalla norma (è possibile una patologia).

Oltre agli indicatori di variazione espressi in valori assoluti, la ricerca statistica utilizza indicatori di variazione espressi in valori relativi. Coefficiente di oscillazione - questo è il rapporto tra l'intervallo di variazione e il valore medio del tratto. Il coefficiente di variazione - questo è il rapporto tra la deviazione standard e il valore medio della caratteristica. Tipicamente, questi valori sono espressi in percentuale.

Formule per il calcolo degli indicatori di variazione relativa:

Dalle formule di cui sopra è chiaro che maggiore è il coefficiente V è più vicino allo zero tanto minore è la variazione dei valori della caratteristica. Più V, tanto più variabile è il segno.

Nella pratica statistica, viene spesso utilizzato il coefficiente di variazione. Viene utilizzato non solo per una valutazione comparativa della variazione, ma anche per caratterizzare l'omogeneità della popolazione. La popolazione è considerata omogenea se il coefficiente di variazione non supera il 33% (per distribuzioni prossime alla normale). Aritmeticamente, il rapporto tra σ e la media aritmetica neutralizza l'influenza del valore assoluto di queste caratteristiche e il rapporto percentuale rende il coefficiente di variazione un valore adimensionale (senza nome).

Il valore risultante del coefficiente di variazione è stimato secondo le gradazioni approssimative del grado di diversità del tratto:

Debole - fino al 10%

Media - 10 - 20%

Forte - più del 20%

L'utilizzo del coefficiente di variazione è consigliabile nei casi in cui sia necessario confrontare caratteristiche diverse per grandezza e dimensione.

La differenza tra il coefficiente di variazione e altri criteri di dispersione è chiaramente dimostrata esempio.

Tabella 1

Composizione degli addetti alle imprese industriali

Sulla base delle caratteristiche statistiche fornite nell’esempio, possiamo trarre una conclusione sulla relativa omogeneità della composizione per età e del livello di istruzione dei dipendenti dell’impresa, data la scarsa stabilità professionale del contingente intervistato. È facile vedere che un tentativo di giudicare queste tendenze sociali mediante la deviazione standard porterebbe a una conclusione errata, e un tentativo di confrontare le caratteristiche contabili “esperienza lavorativa” ed “età” con l’indicatore contabile “istruzione” sarebbe generalmente inefficace. errata a causa dell’eterogeneità di queste caratteristiche.

Mediana e percentili

Per le distribuzioni ordinali (di rango), dove il criterio per la metà della serie è la mediana, la deviazione standard e la dispersione non possono servire come caratteristiche della dispersione della variante.

Lo stesso vale per le serie a variazione aperta. Questa circostanza è dovuta al fatto che gli scostamenti da cui si calcola la varianza e σ sono misurati dalla media aritmetica, che non viene calcolata nelle serie di variazioni aperte e nelle serie di distribuzioni di caratteristiche qualitative. Pertanto, per una descrizione compressa delle distribuzioni, viene utilizzato un altro parametro di dispersione: quantile(sinonimo - “percentile”), adatto a descrivere caratteristiche qualitative e quantitative in qualsiasi forma della loro distribuzione. Questo parametro può essere utilizzato anche per convertire le caratteristiche quantitative in qualitative. In questo caso, tali rating vengono assegnati in base all'ordine di quantile a cui corrisponde una particolare opzione.

Nella pratica della ricerca biomedica, vengono spesso utilizzati i seguenti quantili:

– mediana;

, – quartili (quarti), dove – quartile inferiore, – quartile superiore.

I quantili dividono l'area dei possibili cambiamenti in una serie di variazioni in determinati intervalli. Mediana (quantile) è un'opzione che si trova nel mezzo di una serie di variazioni e divide questa serie a metà in due parti uguali ( 0,5 E 0,5 ). Un quartile divide una serie in quattro parti: la prima parte (quartile inferiore) è un'opzione che separa le opzioni i cui valori numerici non superano il 25% del massimo possibile in una determinata serie; un quartile separa le opzioni con un valore numerico pari a fino al 50% del massimo possibile. Il quartile superiore () separa le opzioni fino al 75% dei valori massimi possibili.

In caso di distribuzione asimmetrica variabile rispetto alla media aritmetica, per caratterizzarla si utilizzano la mediana e i quartili. In questo caso, viene utilizzata la seguente forma di visualizzazione del valore medio: Mah (;). Per esempio, la caratteristica studiata – “il periodo in cui il bambino ha iniziato a camminare in modo indipendente” – ha una distribuzione asimmetrica nel gruppo di studio. Allo stesso tempo, il quartile inferiore () corrisponde all'inizio del cammino - 9,5 mesi, la media - 11 mesi, il quartile superiore () - 12 mesi. Di conseguenza, la caratteristica della tendenza media dell'attributo specificato sarà presentata come 11 (9,5; 12) mesi.

Valutazione della significatività statistica dei risultati dello studio

Per significatività statistica dei dati si intende il grado di corrispondenza con la realtà visualizzata, vale a dire i dati statisticamente significativi sono quelli che non distorcono e riflettono correttamente la realtà oggettiva.

Valutare la significatività statistica dei risultati della ricerca significa determinare con quale probabilità è possibile trasferire i risultati ottenuti dalla popolazione campione all'intera popolazione. Valutare la significatività statistica è necessario per capire quanto di un fenomeno può essere utilizzato per giudicare il fenomeno nel suo insieme e i suoi modelli.

La valutazione della significatività statistica dei risultati della ricerca consiste in:

1. errori di rappresentatività (errori di valori medi e relativi) - M;

2. limiti di confidenza dei valori medi o relativi;

3. affidabilità della differenza nei valori medi o relativi secondo il criterio T.

Errore standard della media aritmetica O errore di rappresentatività caratterizza le fluttuazioni della media. Va notato che maggiore è la dimensione del campione, minore è la diffusione dei valori medi. L'errore standard della media si calcola utilizzando la formula:

Nella letteratura scientifica moderna, la media aritmetica viene scritta insieme all’errore di rappresentatività:

o insieme alla deviazione standard:

Ad esempio, consideriamo i dati su 1.500 cliniche cittadine nel paese (popolazione generale). Il numero medio di pazienti serviti nella clinica è di 18.150 persone. La selezione casuale del 10% dei siti (150 cliniche) dà un numero medio di pazienti pari a 20.051 persone. L'errore di campionamento, ovviamente dovuto al fatto che non tutte le 1500 cliniche sono state incluse nel campione, è pari alla differenza tra queste medie - la media generale ( M gene) e media campionaria ( M selezionato). Se formiamo un altro campione della stessa dimensione dalla nostra popolazione, darà un valore di errore diverso. Tutte queste medie campionarie, con campioni sufficientemente grandi, sono distribuite normalmente attorno alla media generale con un numero sufficientemente elevato di ripetizioni del campione dello stesso numero di oggetti della popolazione generale. Errore standard della media M- questa è l'inevitabile diffusione delle medie campionarie attorno alla media generale.

Nel caso in cui i risultati della ricerca siano presentati in quantità relative (ad esempio percentuali), vengono calcolati errore standard della frazione:

dove P è l'indicatore in %, n è il numero di osservazioni.

Il risultato viene visualizzato come (P±m)%. Per esempio, la percentuale di recupero tra i pazienti è stata (95,2±2,5)%.

Nel caso in cui il numero di elementi della popolazione, quindi quando si calcolano gli errori standard della media e della frazione al denominatore della frazione, invece dideve essere posizionato.

Per una distribuzione normale (la distribuzione delle medie campionarie è normale), sappiamo quale porzione della popolazione rientra in qualsiasi intervallo attorno alla media. In particolare:

In pratica il problema è che le caratteristiche della popolazione generale ci sono sconosciute, e il campione è realizzato proprio allo scopo di stimarle. Ciò significa che se realizziamo campioni della stessa dimensione N dalla popolazione generale, quindi nel 68,3% dei casi l'intervallo conterrà il valore M(nel 95,5% dei casi sarà nell'intervallo e nel 99,7% dei casi – nell'intervallo).

Poiché in realtà viene prelevato un solo campione, questa affermazione viene formulata in termini di probabilità: con una probabilità del 68,3%, il valore medio dell'attributo nella popolazione rientra nell'intervallo, con una probabilità del 95,5% - nell'intervallo, ecc.

In pratica, attorno al valore campionario viene costruito un intervallo tale che, con una data probabilità (sufficientemente alta), probabilità di confidenza –“coprirebbe” il vero valore di questo parametro nella popolazione generale. Questo intervallo è chiamato intervallo di confidenza.

Probabilità di fiduciaP – questo è il grado di confidenza che l'intervallo di confidenza conterrà effettivamente il vero valore (sconosciuto) del parametro nella popolazione.

Ad esempio, se la probabilità di confidenza Rè del 90%, ciò significa che 90 campioni su 100 daranno la stima corretta del parametro nella popolazione. Di conseguenza, la probabilità di errore, ad es. stima errata della media generale del campione è pari in percentuale: . Per questo esempio, ciò significa che 10 campioni su 100 forniranno una stima errata.

Ovviamente, il grado di confidenza (probabilità di confidenza) dipende dalla dimensione dell'intervallo: più ampio è l'intervallo, maggiore è la confidenza che vi rientri un valore sconosciuto per la popolazione. In pratica, viene utilizzato almeno il doppio dell'errore di campionamento per costruire un intervallo di confidenza che fornisca una confidenza pari ad almeno il 95,5%.

Determinare i limiti di confidenza delle medie e dei valori relativi ci consente di trovare i loro due valori estremi: il minimo possibile e il massimo possibile, entro i quali l'indicatore studiato può verificarsi nell'intera popolazione. Basato su questo, limiti di confidenza (o intervallo di confidenza)- questi sono i limiti dei valori medi o relativi, oltre i quali a causa di fluttuazioni casuali esiste una probabilità insignificante.

L'intervallo di confidenza può essere riscritto come: , dove T– criterio di fiducia.

I limiti di confidenza della media aritmetica della popolazione sono determinati dalla formula:

M gene =M Selezionare + t m M

per valore relativo:

R gene = p Selezionare + t m R

Dove M gene E R gene- valori medi e valori relativi per la popolazione generale; M Selezionare E R Selezionare- valori di media e valori relativi ottenuti dalla popolazione campione; M M E M P- errori dei valori medi e relativi; T- criterio di confidenza (criterio di accuratezza, che viene stabilito in fase di pianificazione dello studio e può essere pari a 2 o 3); t m- questo è un intervallo di confidenza o Δ - l'errore massimo dell'indicatore ottenuto in uno studio campione.

Va notato che il valore del criterio T in una certa misura è correlata alla probabilità di una previsione priva di errori (p), espressa in %. Viene scelto dal ricercatore stesso, guidato dalla necessità di ottenere il risultato con il grado di accuratezza richiesto. Pertanto, per la probabilità di una previsione priva di errori pari al 95,5%, il valore del criterio Tè 2, per il 99,7% - 3.

Le stime dell'intervallo di confidenza fornite sono accettabili solo per popolazioni statistiche con più di 30 osservazioni. Con una popolazione di dimensioni inferiori (piccoli campioni), vengono utilizzate tabelle speciali per determinare il criterio t. In queste tabelle, il valore desiderato si trova all'intersezione della linea corrispondente alla dimensione della popolazione (n-1) e una colonna corrispondente al livello di probabilità di una previsione priva di errori (95,5%; 99,7%) scelto dal ricercatore. Nella ricerca medica, quando si stabiliscono limiti di confidenza per qualsiasi indicatore, la probabilità di una previsione priva di errori è pari o superiore al 95,5%. Ciò significa che il valore dell'indicatore ottenuto dalla popolazione campione deve essere riscontrabile nella popolazione generale almeno nel 95,5% dei casi.

Domande sull'argomento della lezione:

Rilevanza degli indicatori di diversità dei tratti in una popolazione statistica.

Caratteristiche generali degli indicatori di variazione assoluta.

Deviazione standard, calcolo, applicazione.

Misure relative di variazione.

Punteggio mediano, quartile.

Valutazione della significatività statistica dei risultati dello studio.

Errore standard della media aritmetica, formula di calcolo, esempio di utilizzo.

Calcolo della proporzione e suo errore standard.

Il concetto di probabilità di confidenza, un esempio di utilizzo.

10. Il concetto di intervallo di confidenza, sua applicazione.

Testare le attività sull'argomento con risposte standard:

1. INDICATORI ASSOLUTI DI VARIAZIONE RELATIVI

1) coefficiente di variazione

2) coefficiente di oscillazione

4) mediana

2. INDICATORI RELATIVI DI VARIAZIONE RELATIVI

1) dispersione

4) coefficiente di variazione

3. CRITERIO DETERMINATO DAI VALORI ESTREMI DI UN'OPZIONE IN UNA SERIE DI VARIAZIONI

2) ampiezza

3) dispersione

4) coefficiente di variazione

4. LA DIFFERENZA DELLE OPZIONI ESTREME È

2) ampiezza

3) deviazione standard

4) coefficiente di variazione

5. IL QUADRATO MEDIO DEGLI SCOSTAMENTI DEI SINGOLI VALORI DI UNA CARATTERISTICA RISPETTO AI SUOI VALORI MEDI È

1) coefficiente di oscillazione

2) mediana

3) dispersione

6. IL RAPPORTO TRA LA SCALA DI VARIAZIONE E IL VALORE MEDIO DI UN CARATTERE È

1) coefficiente di variazione

2) deviazione standard

4) coefficiente di oscillazione

7. IL RAPPORTO TRA LO DEVIAZIONE QUADRATA MEDIA E IL VALORE MEDIO DI UNA CARATTERISTICA È

1) dispersione

2) coefficiente di variazione

3) coefficiente di oscillazione

4) ampiezza

8. L'OPZIONE CHE SI TROVA AL CENTRO DELLA SERIE DI VARIAZIONI E LA DIVIDE IN DUE PARTI UGUALI È

1) mediana

3) ampiezza

9. NELLA RICERCA MEDICA, QUANDO STABILISCONO I LIMITI DI CONFIDENZA DI UN QUALSIASI INDICATORE, SI ACCETTA LA PROBABILITÀ DI UNA PREVISIONE PRIVA DI ERRORI

10. SE 90 CAMPIONI SU 100 DANNO LA STIMA CORRETTA DI UN PARAMETRO NELLA POPOLAZIONE, CIÒ SIGNIFICA CHE LA PROBABILITÀ DI CONFIDENZA P PARI

11. SE 10 CAMPIONI SU 100 DANNO UNA STIMA ERRATA, LA PROBABILITÀ DI ERRORE È PARI

12. LIMITI DI VALORI MEDI O RELATIVI, SUPERARE I QUALI A CAUSA DI OSCILLAZIONI CASUALI HA UNA PROBABILITÀ INSOLVIBILE – QUESTO È

1) intervallo di confidenza

2) ampiezza

4) coefficiente di variazione

13. È CONSIDERATO UN PICCOLO CAMPIONE QUELLA POPOLAZIONE IN QUALE

1) n è inferiore o uguale a 100

2) n è inferiore o uguale a 30

3) n è inferiore o uguale a 40

4) n è vicino a 0

14. PER LA PROBABILITÀ DI UNA PREVISIONE SENZA ERRORI VALORE CRITERIO 95% TÈ

15. PER LA PROBABILITÀ DI UNA PREVISIONE SENZA ERRORI VALORE CRITERIO 99% TÈ

16. PER DISTRIBUZIONI VICINE ALLA NORMALE, LA POPOLAZIONE È CONSIDERATA OMOGENEA SE IL COEFFICIENTE DI VARIAZIONE NON SUPERA

17. OPZIONE, OPZIONI DI SEPARAZIONE, I CUI VALORI NUMERICI NON SUPERANO IL 25% DEL MASSIMO POSSIBILE IN UNA DATA SERIE - QUESTO È

2) quartile inferiore

3) quartile superiore

4) quartile

18. I DATI CHE NON ALTERANO E RIFLETTONO CORRETTAMENTE LA REALTÀ OGGETTIVA SI CHIAMANO

1) impossibile

2) ugualmente possibile

3) affidabile

4) casuale

19. SECONDO LA REGOLA DEI "TRE Sigma", CON DISTRIBUZIONE NORMALE DI UNA CARATTERISTICA ALL'INTERNO
SARÀ LOCALIZZATO

1) Opzione 68,3%.

Aspettativa e varianza

Misuriamo una variabile casuale N volte, ad esempio, misuriamo la velocità del vento dieci volte e vogliamo trovare il valore medio. In che modo il valore medio è correlato alla funzione di distribuzione?

Lanceremo i dadi un gran numero di volte. Il numero di punti che appariranno sui dadi ad ogni lancio è una variabile casuale e può assumere qualsiasi valore naturale compreso tra 1 e 6. Anche la media aritmetica dei punti persi calcolata per tutti i lanci di dado è una variabile casuale, ma per grandi N tende a un numero molto specifico: l'aspettativa matematica Mx. In questo caso Mx = 3,5.

Come hai ottenuto questo valore? Far entrare N test, una volta ottenuto 1 punto, una volta ottenuti 2 punti e così via. Poi quando N→ ∞ numero di risultati in cui è stato lanciato un punto, Allo stesso modo, Quindi

Modello 4.5. Dado

Supponiamo ora di conoscere la legge di distribuzione della variabile casuale X, cioè sappiamo che la variabile casuale X può assumere valori X 1 , X 2 , ..., xk con probabilità P 1 , P 2 , ..., pk.

Valore atteso Mx variabile casuale X equivale:

Risposta. 2,8.

L'aspettativa matematica non è sempre una stima ragionevole di qualche variabile casuale. Quindi, per stimare lo stipendio medio, è più ragionevole utilizzare il concetto di mediana, cioè un valore tale che il numero di persone che ricevono uno stipendio inferiore alla media e uno superiore coincidano.

Mediano una variabile casuale è un numero X 1/2 è tale P (X < X 1/2) = 1/2.

In altre parole, la probabilità P 1 che la variabile casuale X sarà più piccolo X 1/2 e probabilità P 2 che la variabile casuale X sarà maggiore X 1/2 sono identici e uguali a 1/2. La mediana non è determinata univocamente per tutte le distribuzioni.

Torniamo alla variabile casuale X, che può assumere valori X 1 , X 2 , ..., xk con probabilità P 1 , P 2 , ..., pk.

Varianza variabile casuale X Il valore medio della deviazione al quadrato di una variabile casuale dalla sua aspettativa matematica è chiamato:

Esempio 2

Nelle condizioni dell'esempio precedente, calcola la varianza e la deviazione standard della variabile casuale X.

Risposta. 0,16, 0,4.

Modello 4.6. Sparare a un bersaglio

Esempio 3

Trova la distribuzione di probabilità del numero di punti ottenuti al primo lancio di dadi, la mediana, l'aspettativa matematica, la varianza e la deviazione standard.

Qualsiasi bordo ha la stessa probabilità di cadere, quindi la distribuzione sarà simile a questa:

Deviazione standard Si può vedere che la deviazione del valore dal valore medio è molto ampia.

Proprietà dell'aspettativa matematica:

L'aspettativa matematica della somma di variabili casuali indipendenti è uguale alla somma delle loro aspettative matematiche:

Esempio 4

Trova l'aspettativa matematica della somma e del prodotto dei punti lanciati su due dadi.

Nell'esempio 3 lo abbiamo trovato per un cubo M (X) = 3,5. Quindi, per due cubi

Proprietà di dispersione:

La varianza della somma di variabili casuali indipendenti è uguale alla somma delle varianze:

Dx + sì = Dx + Dy.

Lasciamo perdere N rotola sui dadi lanciati sì punti. Poi

Questo risultato è vero non solo per i tiri di dado. In molti casi, determina l'accuratezza della misurazione empirica dell'aspettativa matematica. Lo si può vedere con l’aumentare del numero di misurazioni N la diffusione dei valori attorno alla media, cioè la deviazione standard, diminuisce proporzionalmente

La varianza di una variabile casuale è legata all'aspettativa matematica del quadrato di questa variabile casuale dalla seguente relazione:

Troviamo le aspettative matematiche di entrambi i lati di questa uguaglianza. A priori,

L'aspettativa matematica del lato destro dell'uguaglianza, secondo la proprietà delle aspettative matematiche, è uguale a

Deviazione standard

Deviazione standard uguale alla radice quadrata della varianza:
Quando si determina la deviazione standard per un volume sufficientemente ampio della popolazione studiata (n > 30), vengono utilizzate le seguenti formule:

Informazioni correlate.

Risposte alle domande d'esame sulla sanità pubblica e l'assistenza sanitaria.
1. La sanità pubblica e l'assistenza sanitaria come scienza e area di attività pratica. Obiettivi principali. Oggetto, oggetto di studio. Metodi.
2. Sanità. Definizione. Storia dello sviluppo sanitario. I moderni sistemi sanitari, le loro caratteristiche.
3. Politica statale nel campo della tutela della salute pubblica (Legge della Repubblica di Bielorussia “Sulla sanità”). Principi organizzativi del sistema sanitario pubblico.
4. Assicurazioni e forme private di sanità.
5. Prevenzione, definizione, principi, problemi moderni. Tipologie, livelli, indicazioni di prevenzione.
6. Programmi nazionali di prevenzione. Il loro ruolo nel migliorare la salute pubblica.
7. Etica e deontologia medica. Definizione del concetto. Problemi moderni di etica e deontologia medica, caratteristiche.
8. Stile di vita sano, definizione del concetto. Aspetti sociali e medici di uno stile di vita sano (stile di vita sano).
9. Formazione ed educazione igienica, definizione, principi fondamentali. Metodi e mezzi di formazione ed educazione igienica. Requisiti per la lezione, bollettino sanitario.
10. Salute della popolazione, fattori che influenzano la salute pubblica. Formula sanitaria. Indicatori caratterizzanti la sanità pubblica. Schema di analisi.
11. La demografia come scienza, definizione, contenuti. L’importanza dei dati demografici per l’assistenza sanitaria.
12. Statistica demografica, metodi di studio. Censimento della popolazione. Tipi di strutture per età della popolazione.
13. Movimento meccanico della popolazione. Caratteristiche dei processi migratori, loro impatto sugli indicatori di salute della popolazione.
14. La fertilità come problema medico e sociale. Metodologia per il calcolo degli indicatori. Livelli di fertilità secondo i dati dell'OMS. Tendenze moderne.
15. Indicatori speciali di fertilità (indicatori di fertilità). Riproduzione della popolazione, tipi di riproduzione. Indicatori, metodi di calcolo.
16. La mortalità come problema medico e sociale. Metodologia di studio, indicatori. Livelli complessivi di mortalità secondo i dati dell’OMS. Tendenze moderne.
17. La mortalità infantile come problema medico e sociale. Fattori che ne determinano il livello.
18. Mortalità materna e perinatale, principali cause. Indicatori, metodi di calcolo.
19. Movimento naturale della popolazione, fattori che lo influenzano. Indicatori, metodi di calcolo. Modelli di base del movimento naturale in Bielorussia.
20. Pianificazione familiare. Definizione. Problemi moderni. Organizzazioni mediche e servizi di pianificazione familiare nella Repubblica di Bielorussia.
21. La morbilità come problema medico e sociale. Tendenze e caratteristiche moderne nella Repubblica di Bielorussia.
22. Aspetti medici e sociali della salute neuropsichica della popolazione. Organizzazione dell'assistenza psiconeurologica
23. Alcolismo e tossicodipendenza come problema medico e sociale
24. Le malattie del sistema circolatorio come problema medico e sociale. Fattori di rischio. Indicazioni di prevenzione. Organizzazione dell'assistenza cardiaca.
25. Le neoplasie maligne come problema medico e sociale. Principali direzioni di prevenzione. Organizzazione dell'assistenza oncologica.
26. Classificazione statistica internazionale delle malattie. Principi costruttivi, modalità d'uso. Il suo significato nello studio della morbilità e della mortalità della popolazione.
27. Metodi per studiare la morbilità della popolazione, loro caratteristiche comparative.
Metodologia per lo studio della morbilità generale e primaria
Indicatori di morbilità generale e primaria.
Indicatori di morbilità infettiva.
Principali indicatori che caratterizzano le più importanti morbilità non epidemiche.
Principali indicatori di morbilità “ospedalizzata”:
4) Malattie con invalidità temporanea (domanda 30)
Principali indicatori per l'analisi della morbilità con VUT.
31. Studio della morbilità secondo esami preventivi della popolazione, tipologie di esami preventivi, procedura. Gruppi sanitari. Il concetto di “affezione patologica”.
32. Morbilità secondo i dati sulle cause di morte. Metodologia di studio, indicatori. Certificato medico di morte.
Principali indicatori di morbilità basati sulle cause di morte:
33. La disabilità come problema medico e sociale Definizione del concetto, indicatori. Tendenze della disabilità nella Repubblica di Bielorussia.
Tendenze della disabilità nella Repubblica di Bielorussia.
34. Assistenza sanitaria primaria (PHC), definizione, contenuto, ruolo e collocazione nel sistema sanitario pubblico. Funzioni principali.
35. Principi fondamentali dell'assistenza sanitaria primaria. Organizzazioni mediche di assistenza sanitaria primaria.
36. Organizzazione delle cure mediche fornite alla popolazione in regime ambulatoriale. Principi di base. Istituzioni.
37. Organizzazione dell'assistenza medica in ambito ospedaliero. Istituzioni. Indicatori dell'erogazione delle cure ospedaliere.
38. Tipologie di cure mediche. Organizzazione delle cure mediche specialistiche per la popolazione. Centri di assistenza medica specialistica, i loro compiti.
39. Principali direzioni per migliorare l'assistenza ospedaliera e specialistica nella Repubblica di Bielorussia.
40. Tutela della salute delle donne e dei bambini nella Repubblica di Bielorussia. Controllo. Organizzazioni mediche.
41. Problemi moderni della salute della donna. Organizzazione dell'assistenza ostetrica e ginecologica nella Repubblica di Bielorussia.
42. Organizzazione delle cure mediche e preventive per i bambini. Principali problemi di salute dei bambini.
43. Organizzazione dell'assistenza sanitaria per la popolazione rurale, principi di base per fornire assistenza medica ai residenti rurali. Fasi. Organizzazioni.
Fase II – Associazione Medica Territoriale (TMO).
Fase III – ospedale regionale e istituzioni mediche regionali.
45. Esame medico sociale (MSE), definizione, contenuti, concetti base.
46. Riabilitazione, definizione, tipologie. Legge della Repubblica di Bielorussia “Sulla prevenzione della disabilità e sulla riabilitazione delle persone con disabilità”.
47. Riabilitazione medica: definizione del concetto, fasi, principi. Servizio di riabilitazione medica nella Repubblica di Bielorussia.
48. Ambulatorio cittadino, struttura, compiti, gestione. Indicatori chiave di prestazione della clinica.
Indicatori chiave di prestazione della clinica.
49. Il principio locale di organizzazione dell'assistenza ambulatoriale per la popolazione. Tipi di trame. Area terapeutica territoriale. Standard. Contenuti del lavoro di un medico-terapeuta locale.
Organizzazione del lavoro di un terapista locale.
50. Ufficio malattie infettive della clinica. Sezioni e metodi di lavoro di un medico nell'ufficio di malattie infettive.
52. Principali indicatori che caratterizzano la qualità e l'efficacia dell'osservazione dispensaria. Metodo del loro calcolo.
53. Dipartimento di riabilitazione medica (MR) della clinica. Struttura, compiti. La procedura per indirizzare i pazienti all'OMR.
54. Clinica pediatrica, struttura, compiti, sezioni di lavoro. Caratteristiche della fornitura di assistenza medica ai bambini in ambito ambulatoriale.
55. Le sezioni principali del lavoro di un pediatra locale. Contenuti del trattamento e del lavoro preventivo. Comunicazione nel lavoro con altre istituzioni di cura e prevenzione. Documentazione.
56. Contenuti del lavoro preventivo di un pediatra locale. Organizzazione dell'assistenza infermieristica ai neonati.
57. Struttura, organizzazione, contenuto del lavoro della clinica prenatale. Indicatori di lavoro sul servizio alle donne incinte. Documentazione.
58. Maternità, struttura, organizzazione del lavoro, gestione. Indicatori di prestazione dell'ospedale di maternità. Documentazione.
59. Ospedale cittadino, compiti, struttura, principali indicatori di prestazione. Documentazione.
60. Organizzazione del lavoro del reparto di accoglienza dell'ospedale. Documentazione. Misure di prevenzione delle infezioni nosocomiali. Regime terapeutico e protettivo.
Sezione 1. Informazioni sulle divisioni e sugli impianti dell'organizzazione di trattamento e prevenzione.
Sezione 2. Personale dell'organizzazione di cura e prevenzione alla fine dell'anno di riferimento.
Sezione 3. Lavoro dei medici della clinica (ambulatorio), dispensario, consultazioni.
Sezione 4. Esami medici preventivi e lavoro di studi dentistici (odontoiatrici) e chirurgici di un'organizzazione medica e preventiva.
Sezione 5. Lavoro dei dipartimenti medici e ausiliari (uffici).
Sezione 6. Funzionamento dei reparti diagnostici.
62. Relazione annuale sull'attività dell'ospedale (modulo 14), procedura di allestimento, struttura. Indicatori chiave di prestazione dell'ospedale.
Sezione 1. Composizione dei pazienti ricoverati in ospedale ed esiti del loro trattamento
Sezione 2. Composizione dei neonati malati trasferiti in altri ospedali all'età di 0-6 giorni ed esiti delle loro cure
Sezione 3. Posti letto e suo utilizzo
Sezione 4. Lavoro chirurgico dell'ospedale
63. Relazione sull'assistenza medica alle gestanti, alle partorienti e alle partorienti (f. 32), struttura. Indicatori di base.
Sezione I. Attività della clinica prenatale.
Sezione II. Ostetricia in un ospedale
Sezione III. Mortalità materna
Sezione IV. Informazioni sulle nascite
64. Consulenza genetica medica, principali istituzioni. Il suo ruolo nella prevenzione della mortalità perinatale e infantile.
65. Statistica medica, sue sezioni, compiti. Il ruolo del metodo statistico nello studio della salute della popolazione e della performance del sistema sanitario.
66. Popolazione statistica. Definizione, tipi, proprietà. Caratteristiche della conduzione di ricerche statistiche su una popolazione campione.
67. Popolazione campione, requisiti per essa. Il principio e i metodi per formare una popolazione campione.
68. Unità di osservazione. Definizione, caratteristiche delle caratteristiche contabili.
69. Organizzazione della ricerca statistica. Caratteristiche delle fasi.
70. Contenuti del piano e programma della ricerca statistica. Tipologie di piani di ricerca statistica. Programma di osservazione.
71. Osservazione statistica. Ricerca statistica continua e non continua. Tipi di ricerche statistiche incomplete.
72. Osservazione statistica (raccolta di materiali). Errori nell'osservazione statistica.
73. Raggruppamento statistico e sintesi. Raggruppamento tipologico e variazionale.
74. Tabelle statistiche, tipologie, requisiti costruttivi.

81. Deviazione standard, metodo di calcolo, applicazione.

Un metodo approssimativo per valutare la variabilità di una serie di variazioni consiste nel determinare il limite e l'ampiezza, ma i valori della variante all'interno della serie non vengono presi in considerazione. La principale misura generalmente accettata della variabilità di una caratteristica quantitativa all'interno di una serie di variazioni è deviazione standard (σ -sigma). Maggiore è la deviazione standard, maggiore è il grado di fluttuazione di questa serie.

Il metodo per il calcolo della deviazione standard prevede i seguenti passaggi:

1. Trova la media aritmetica (M).

3. Eleva al quadrato ogni deviazione d 2.

4. Moltiplicare i quadrati delle deviazioni per le frequenze corrispondenti d 2 *p.

5. Trova la somma dei prodotti (d 2 *p)

6. Calcola la deviazione standard utilizzando la formula:

quando n è maggiore di 30, O
quando n è inferiore o uguale a 30, dove n è il numero di tutte le opzioni.

Valore della deviazione standard:

2. La deviazione standard viene utilizzata per una valutazione comparativa del grado di corrispondenza della media aritmetica con la serie di variazioni per la quale è stata calcolata.

È stato stabilito che con una distribuzione normale del tratto:

Il 68,3% dei valori dell'opzione rientra nel M1

Il 95,5% dei valori dell'opzione rientrano nel M2

Il 99,7% dei valori dell’opzione rientrano nel M3

3. La deviazione standard consente di stabilire valori normali per i parametri clinici e biologici. In medicina, l'intervallo M1 viene solitamente considerato l'intervallo normale per il fenomeno studiato. La deviazione del valore stimato dalla media aritmetica superiore a 1 indica una deviazione del parametro studiato dalla norma.

5. La deviazione standard è necessaria per caratterizzare il grado di diversità della caratteristica studiata e per calcolare l'errore della media aritmetica.

Il valore della deviazione standard viene solitamente utilizzato per confrontare la variabilità di serie dello stesso tipo. Se si confrontano due serie con caratteristiche diverse (altezza e peso, durata media del trattamento ospedaliero e mortalità ospedaliera, ecc.), allora un confronto diretto delle dimensioni sigma è impossibile , Perché la deviazione standard è un valore denominato espresso in numeri assoluti. In questi casi, utilizzare il coefficiente di variazione (CV) , che è un valore relativo: il rapporto percentuale tra la deviazione standard e la media aritmetica.

Il coefficiente di variazione si calcola utilizzando la formula: